美团数据库平台研发组,面临日益急迫的数据库异常发现需求,为了更加快速、智能地发现、定位和止损,我们开发了基于AI算法的数据库异常检测服务。本文从特征分析、算法选型、模型训练与实时检测等维度介绍了我们的一些实践和思考,希望为从事相关工作的同学带来一些启发或者帮助。

1. 背景
2. 特征分析
2.1 找出数据的变化规律
3. 算法选型
3.1 分布规律与算法选择
3.2 案例样本建模
4. 模型训练与实时检测
4.1 数据流转过程
4.2 异常检测过程
5. 产品运营
6. 未来展望
7. 附录
7.1 绝对中位差
7.2 箱形图
7.3 极值理论
1. 背景
数据库被广泛用于美团的核心业务场景上,对稳定性要求较高,对异常容忍度非常低。因此,快速的数据库异常发现、定位和止损就变得越来越重要。针对异常监测的问题,传统的固定阈值告警方式,需要依赖专家经验进行规则配置,不能根据不同业务场景灵活动态调整阈值,容易让小问题演变成大故障。 而基于AI的数据库异常发现能力,可以基于数据库历史表现情况,对关键指标进行7*24小时巡检,能够在异常萌芽状态就发现风险,更早地将异常暴露,辅助研发人员在问题恶化前进行定位和止损。基于以上这些因素的考量,美团数据库平台研发组决定开发一套数据库异常检测服务系统。接下来,本文将会从特征分析、算法选型、模型训练与实时检测等几个维度阐述我们的一些思考和实践。
2. 特征分析
2.1 找出数据的变化规律
在具体进行开发编码前,有一项非常重要的工作,就是从已有的历史监控指标中,发现时序数据的变化规律,从而根据数据分布的特点选取合适的算法。以下是我们从历史数据中选取的一些具有代表性的指标分布图:
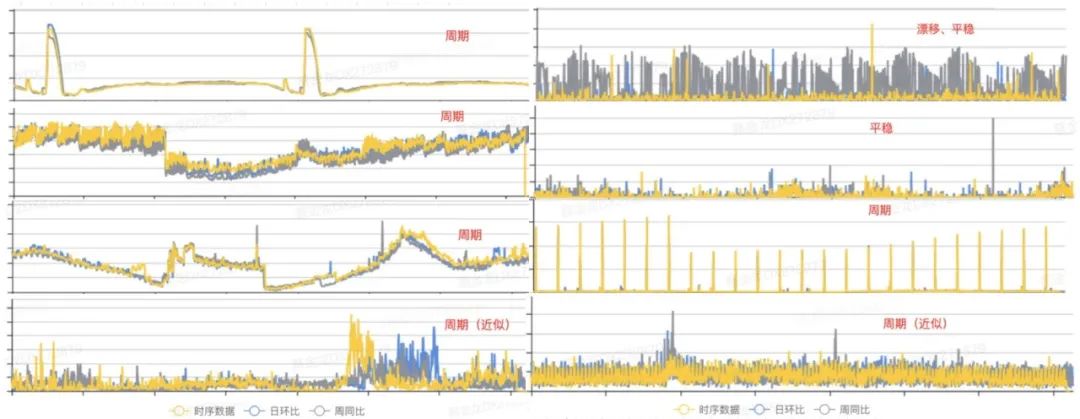
图1 数据库指标形态 从上图我们可以看出,数据的规律主要呈现三种状态:周期、漂移和平稳[1]。因此,我们前期可以针对这些普遍特征的样本进行建模,即可覆盖大部分场景。接下来,我们分别从周期性、漂移性和平稳性这三个角度进行分析,并讨论算法设计的过程。
2.1.1 周期性变化
在很多业务场景中,指标会由于早晚高峰或是一些定时任务引起规律性波动。我们认为这属于数据的内在规律性波动,模型应该具备识别出周期性成分,检测上下文异常的能力。对于不存在长期趋势成分的时序指标而言,当指标存在周期性成分的情况下,,其中T代表的是时序的周期跨度。可通过计算自相关图,即计算出t取不同值时 的值,然后通过分析自相关峰的间隔来确定周期性,主要的流程包括以下几个步骤:
提取趋势成分,分离出残差序列。使用移动平均法提取出长期趋势项,跟原序列作差得到残差序列(此处周期性分析与趋势无关,若不分离趋势成分,自相关将显著受到影响,难以识别周期)。
计算残差的循环自相关(Rolling Correlation)序列。通过循环移动残差序列后,与残差序列进行向量点乘运算来计算自相关序列(循环自相关可以避免延迟衰减)。
根据自相关序列的峰值坐标来确定周期T。提取自相关序列的一系列局部最高峰,取横坐标的间隔为周期(如果该周期点对应的自相关值小于给定阈值,则认为无显著周期性)。
具体过程如下:
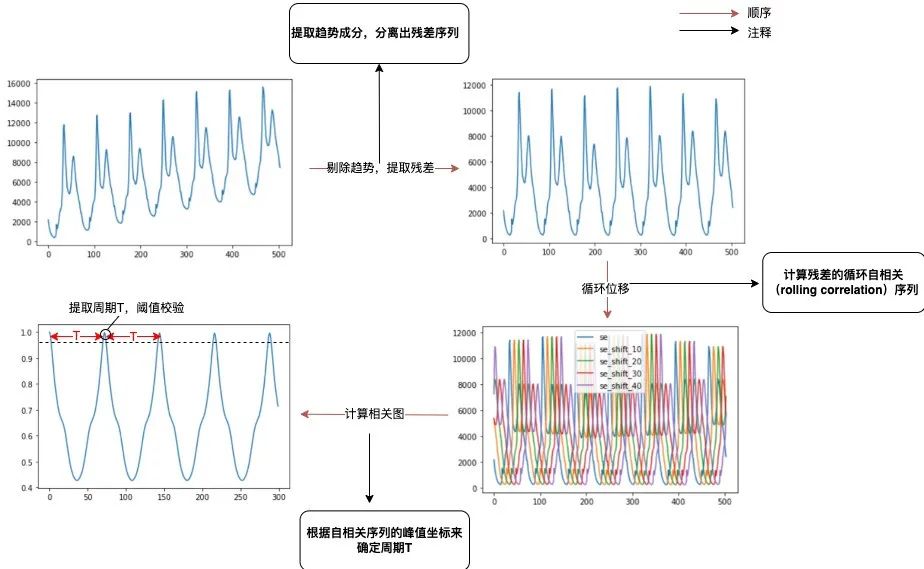
图2 周期提取流程示意
2.1.2 漂移性变化
对于待建模的序列,通常要求它不存在明显的长期趋势或是存在全局漂移的现象,否则生成的模型通常无法很好地适应指标的最新走势[2]。我们将时间序列随着时间的变化出现均值的显著变化或是存在全局突变点的情况,统称为漂移的场景。为了能够准确地捕捉时间序列的最新走势,我们需要在建模前期判断历史数据中是否存在漂移的现象。全局漂移和周期性序列均值漂移,如下示例所示:
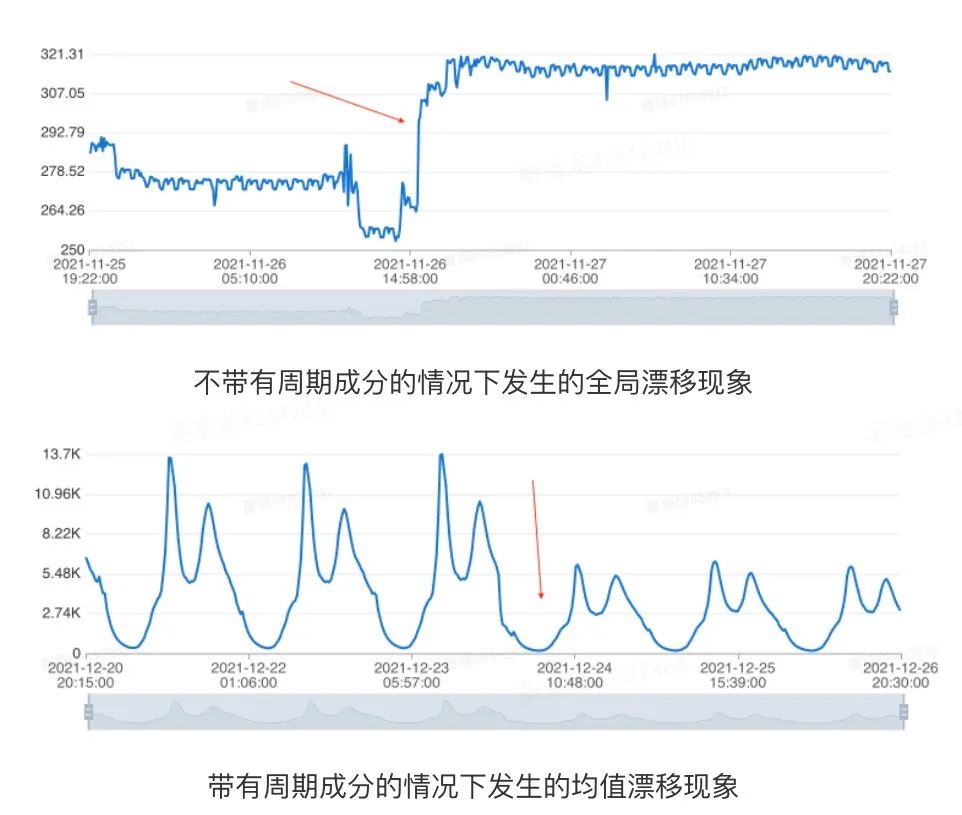
图3 数据漂移示意 数据库指标受业务活动等复杂因素影响,很多数据会有非周期性的变化,而建模需要容忍这些变化。因此,区别于经典的变点检测问题,在异常检测场景下,我们只需要检测出历史上很平稳,之后出现数据漂移的情况。综合算法性能和实际表现,我们使用了基于中位数滤波的漂移检测方法,主要的流程包含以下几个环节: 1. 中位数平滑
a. 根据给定窗口的大小,提取窗口内的中位数来获取时序的趋势成分。
b. 窗口需要足够大,以避免周期因素影响,并进行滤波延迟矫正。
c. 使用中位数而非均值平滑的原因在于为了规避异常样本的影响。
2. 判断平滑序列是否递增或是递减 a. 中位数平滑后的序列数据,若每个点都大于(小于)前一个点,则序列为递增(递减)序列。
b. 如果序列存在严格递增或是严格递减的性质,则指标明显存在长期趋势,此时可提前终止。
3.遍历平滑序列,利用如下两个规则来判断是否存在漂移的现象
a. 当前样本点左边序列的最大值小于当前样本点右边序列的最小值,则存在突增漂移(上涨趋势)。
b. 当前样本点左边序列的最小值大于当前样本点右边序列的最大值,则存在突降漂移(下跌趋势)。
2.1.3 平稳性变化
对于一个时序指标,如果其在任意时刻,它的性质不随观测时间的变化而变化,我们认为这条时序是具备平稳性的。因此,对于具有长期趋势成分亦或是周期性成分的时间序列而言,它们都是不平稳的。具体示例如下图所示:
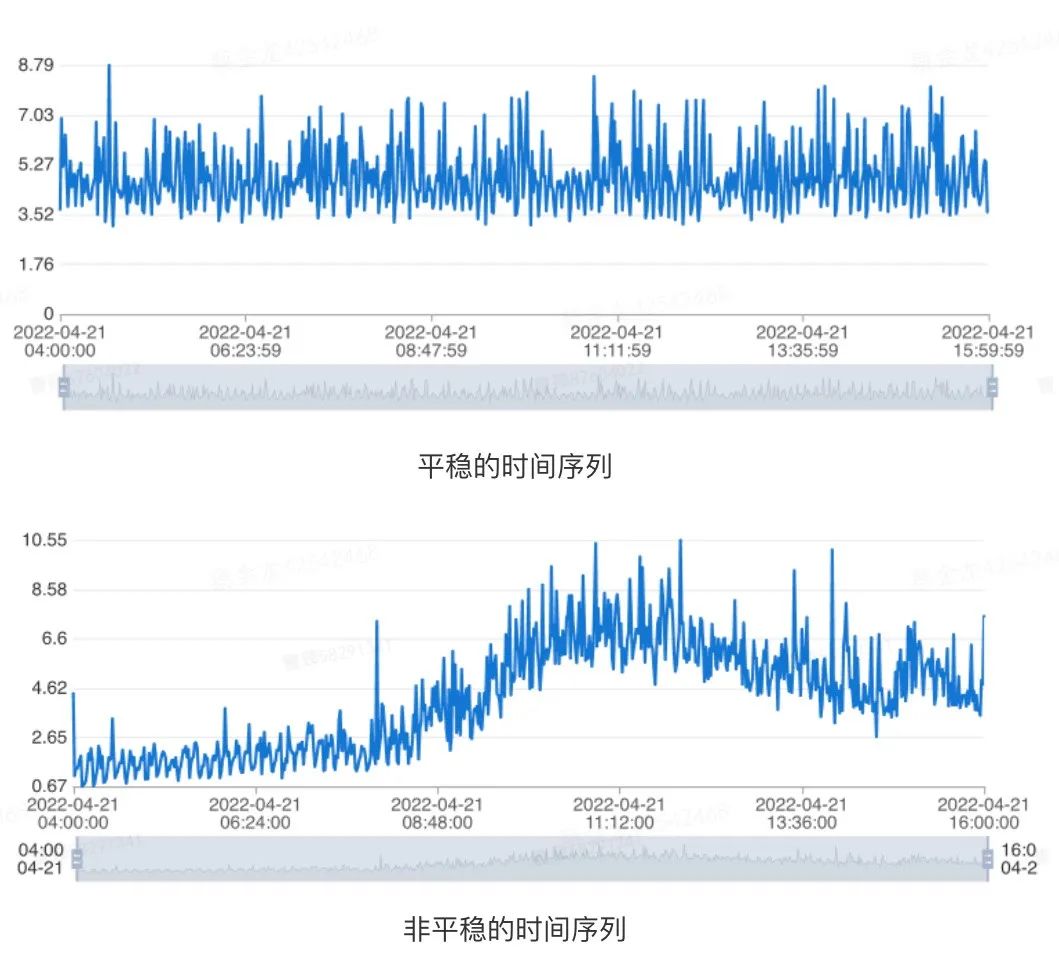
图4 数据平稳示意 针对这种情况,我们可以通过单位根检验(Augmented Dickey-Fuller Test)[3]来判断给定的时间序列是否平稳。具体地说,对于一条给定时间范围指标的历史数据而言,我们认为在同时满足如下条件的情况下,时序是平稳的:
最近1天的时序数据通过adfuller检验获得的p值小于0.05。
最近7天的时序数据通过adfuller检验获得的p值小于0.05。
3. 算法选型
3.1 分布规律与算法选择
通过了解业界的一些知名公司在时序数据异常检测上公布的产品介绍,加上我们历史积累的经验,以及对部分线上实际指标的抽样分析,它们的概率密度函数符合如下情况的分布:
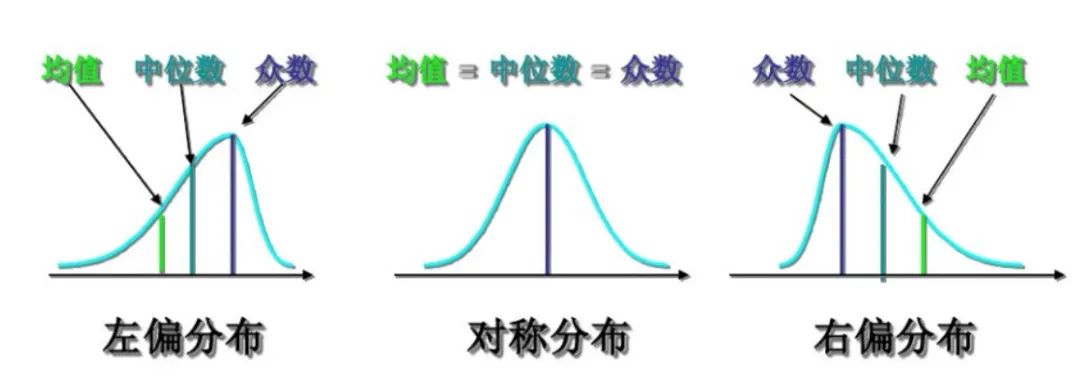
图5 分布偏斜示意 针对上述的分布,我们调研了一些常见的算法,并确定了箱形图、绝对中位差和极值理论作为最终异常检测算法。以下是对常见时序数据检测的算法对比表:
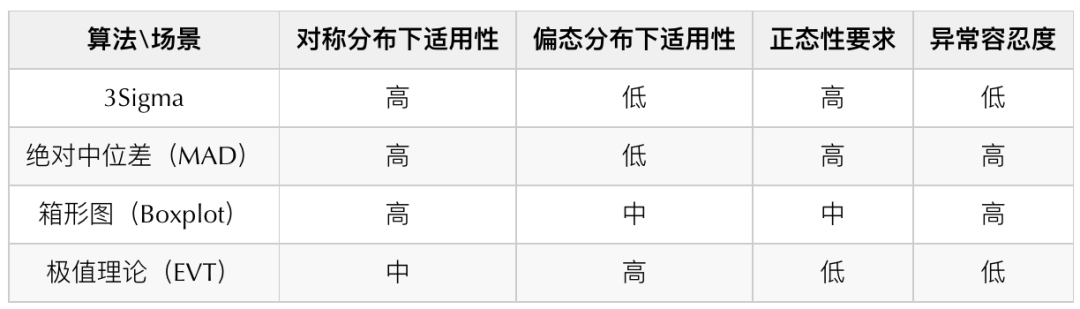
我们没有选择3Sigma的主要原因是它对异常容忍度较低,而绝对中位差从理论上而言具有更好的异常容忍度,所以在数据呈现高对称分布时,通过绝对中位差(MAD)替代3Sigma进行检测。我们对不同数据的分布分别采用了不同的检测算法(关于不同算法的原理可以参考文末附录的部分,这里不做过多的阐述):
低偏态高对称分布:绝对中位差(MAD)
中等偏态分布:箱形图(Boxplot)
高偏态分布:极值理论(EVT)
有了如上的分析,我们可以得出具体的根据样本输出模型的流程:
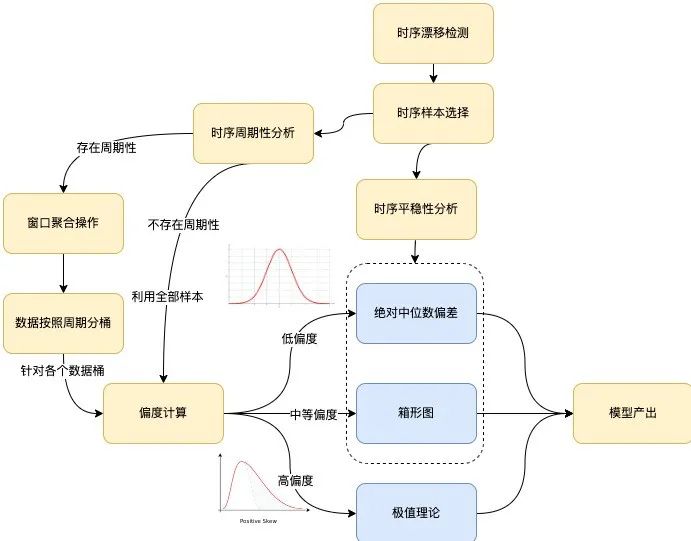
图6 算法建模流程 算法的整体建模流程如上图所示,主要涵盖以下几个分支环节:时序漂移检测、时序平稳性分析、时序周期性分析和偏度计算。下面分别进行介绍:
时序漂移检测。如果检测存在漂移的场景,则需要根据检测获得的漂移点t来切割输入时序,使用漂移点后的时序样本作为后续建模流程的输入,记为S={Si},其中i>t。
时序平稳性分析。如果输入时序S满足平稳性检验,则直接通过箱形图(默认)或是绝对中位差的方式来进行建模。
时序周期性分析。存在周期性的情况下,将周期跨度记为T,将输入时序S根据跨度T进行切割,针对各个时间索引j∈{0,1,⋯,T−1}所组成的数据桶进行建模流程。不存在周期性的情况下,针对全部输入时序S作为数据桶进行建模流程。
案例:给定一条时间序列ts={t0,t1,⋯,tn},假定其存在周期性且周期跨度为T,对于时间索引j而言,其中j∈{0,1,⋯,T−1},对其建模所需要的样本点由区间[tj−kT−m, tj−kT+m]构成,其中m为参数,代表窗口大小,k为整数,满足j−kT−m≥0, j−kT+m≤n。 举例来说,假设给定时序自2022/03/01 0000至2022/03/08 0000止,给定窗口大小为5,周期跨度为一天,那么对于时间索引30而言,对其建模所需要的样本点将来自于如下时间段: [03/01 0000, 03/01 0000] [03/02 0000, 03/02 0000] ... [03/07 0000, 03/07 0000]
偏度计算。时序指标转化为概率分布图,计算分布的偏度,若偏度的绝对值超过阈值,则通过极值理论进行建模输出阈值。若偏度的绝对值小于阈值,则通过箱形图或是绝对中位差的方式进行建模输出阈值。
3.2 案例样本建模
这里选取了一个案例,展示数据分析及建模过程,便于更清晰的理解上述过程。其中图(a)为原始序列,图(b)为按照天的跨度进行折叠的序列,图(c)为图(b)中某时间索引区间内的样本经过放大后的趋势表现,图(d)中黑色曲线为图(c)中时间索引所对应的下阈值。如下是针对某时序的历史样本进行建模的案例:
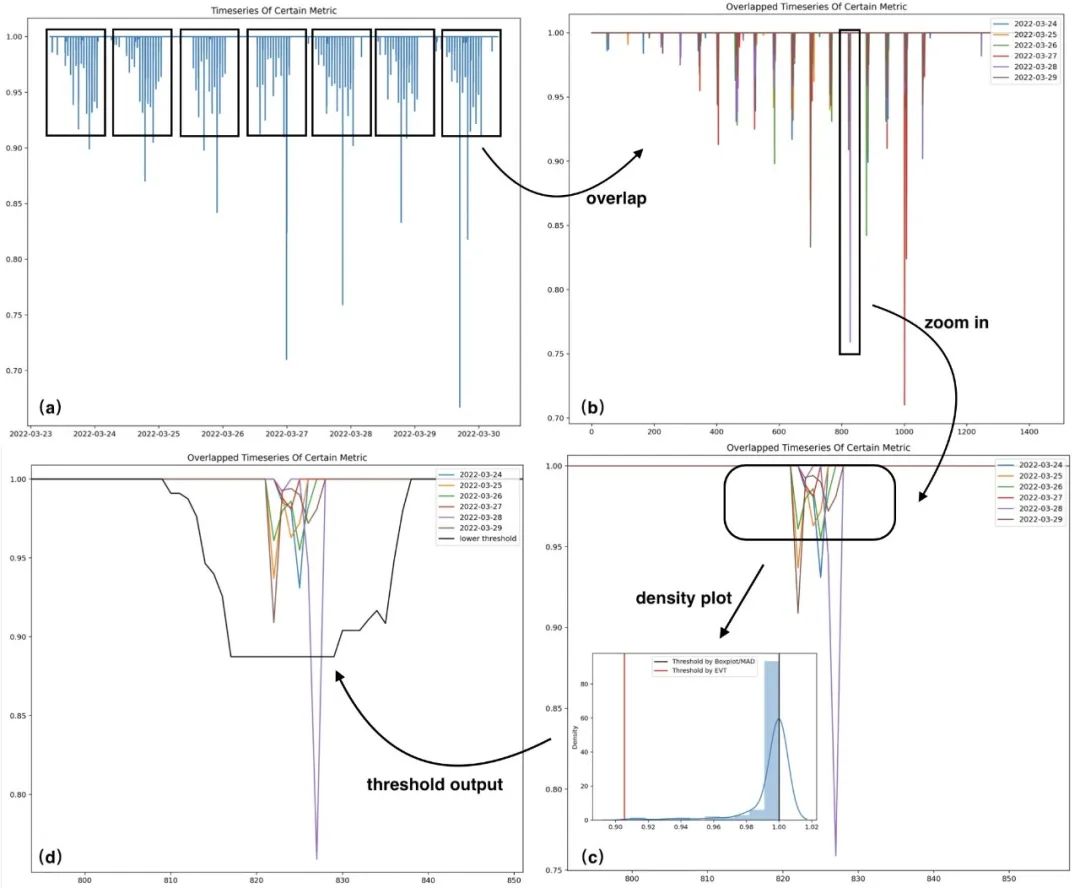
图7 建模案例 上图(c)区域内的样本分布直方图以及阈值(已剔除其中部分异常样本),可以看到,在该高偏分布的场景中,EVT算法计算的阈值更为合理。
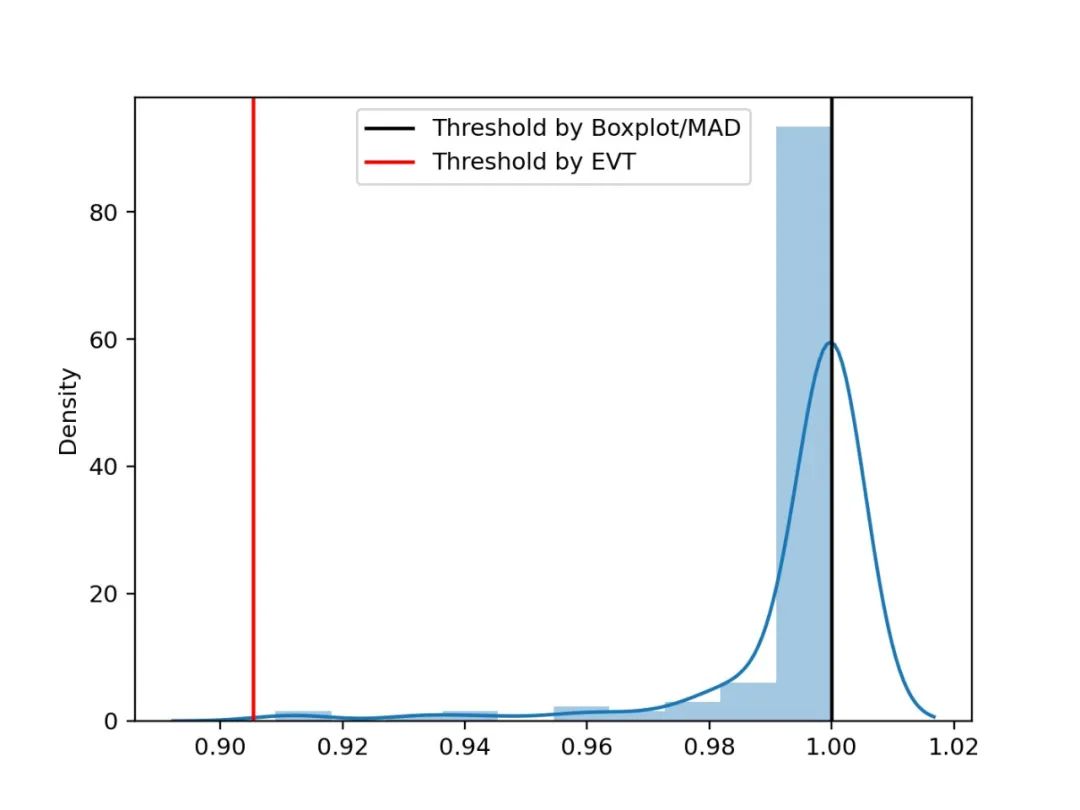
图8 偏斜分布阈值对比
4. 模型训练与实时检测
4.1 数据流转过程
为了实时检测规模庞大的秒级数据,我们以基于Flink进行实时流处理为出发点,设计了如下的技术方案:
实时检测部分:基于Flink实时流处理,消费Mafka(美团内部的消息队列组件)消息进行在线检测,结果存储于Elasticsearch(以下简称ES)中,并产生异常记录。
离线训练部分:以Squirrel(美团内部的KV数据库)作为任务队列,从MOD(美团内部运维数据仓库)读取训练数据,从配置表读取参数,训练模型,保存于ES,支持自动和手动触发训练,通过定时读取模型库的方式,进行模型加载和更新。
以下是具体的离线训练和在线检测技术设计:
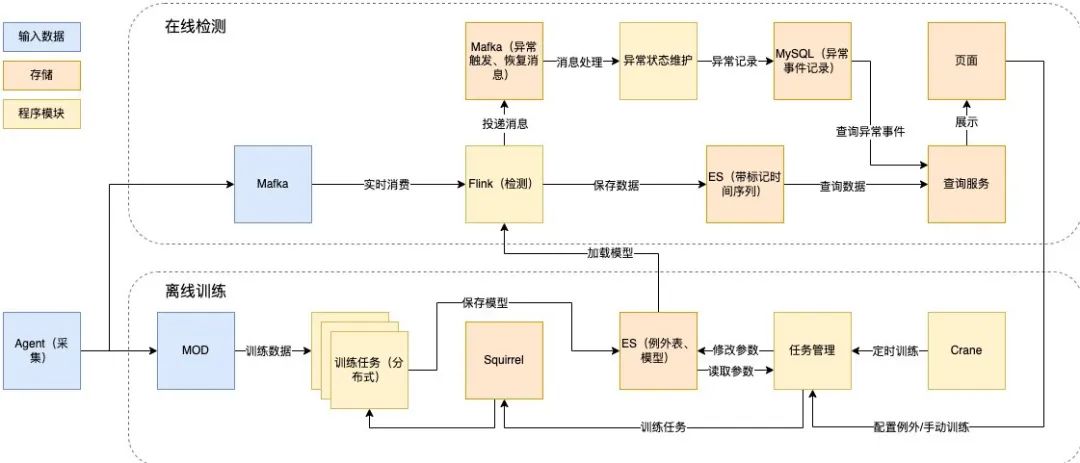
图9 离线训练和在线检测技术设计
4.2 异常检测过程
异常检测算法整体采用分治思想,在模型训练阶段,根据历史数据识别提取特征,选定合适的检测算法。这里分为离线训练和在线检测两部分,离线主要根据历史情况进行数据预处理、时序分类和时序建模。在线主要加载运用离线训练的模型进行在线实时异常检测。具体设计如下图所示:
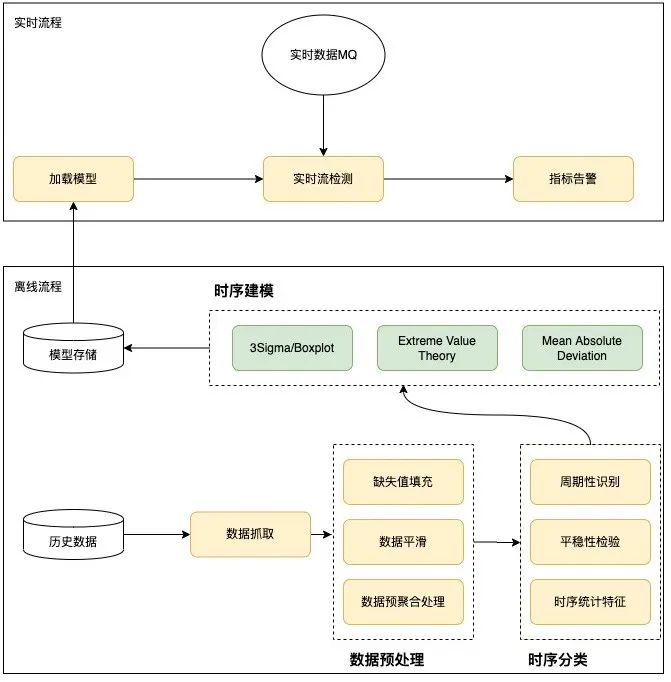
图10 异常检测过程
5. 产品运营
为了提高优化迭代算法的效率,持续运营以提高精准率和召回率,我们借助Horae(美团内部可扩展的时序数据异常检测系统)的案例回溯能力,实现在线检测、案例保存、分析优化、结果评估、发布上线的闭环。
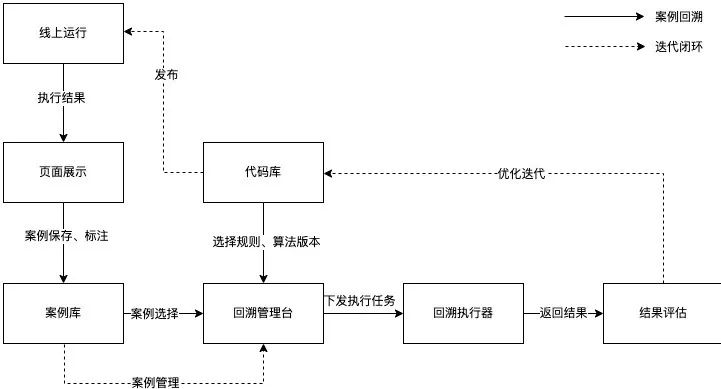
图11 运营流程
目前,异常检测算法指标如下:
精准率:随机选择一部分检测出异常的案例,人工校验其中确实是异常的比例,为81%。
召回率:根据故障、告警等来源,审查对应实例各指标异常情况,对照监测结果计算召回率,为82%。
F1-score:精准率和召回率的调和平均数,为81%。
6. 未来展望
目前,美团数据库异常监测能力已基本构建完成,后续我们将对产品继续进行优化和拓展,具体方向包括:
具有异常类型识别能力。可以检测出异常的类型,如均值变化、波动变化、尖刺等,支持按异常类型进行告警订阅,并作为特征输入后续诊断系统,完善数据库自治生态[4]。
构建Human-in-Loop环境。支持根据反馈标注自动学习,保障模型持续优化[5]。
多种数据库场景的支持。异常检测能力平台化以支持更多数据库场景,如DB端到端报错、节点网络监测等。
7. 附录
7.1 绝对中位差
绝对中位差,即Median Absolute Deviation(MAD),是对单变量数值型数据的样本偏差的一种鲁棒性测量[6],通常由下式计算而得:
其中在先验为正态分布的情况下,一般C选择1.4826,k选择3。MAD假定样本中间的50%区域均为正常样本,而异常样本落在两侧的50%区域内。当样本服从正态分布的情况下,MAD指标相较于标准差更能适应数据集中的异常值。对于标准差,使用的是数据到均值的距离平方,较大的偏差权重较大,异常值对结果影响不能忽视,而对MAD而言少量的异常值不会影响实验的结果,MAD算法对于数据的正态性有较高要求。
7.2 箱形图
箱形图主要通过几个统计量来描述样本分布的离散程度以及对称性,包括:
Q0:最小值(Minimum)
Q1:下四分位数(Lower Quartile)
Q2:中位数(Median)
Q3:上四分位数(Upper Quartile)
Q4:最大值(Maximum)
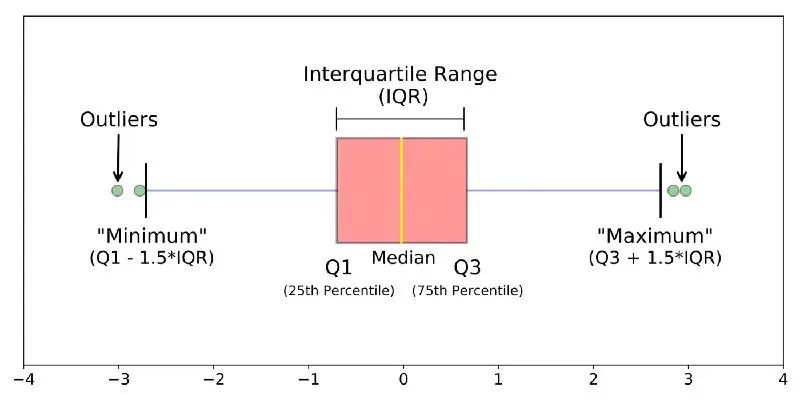
图12 箱线图
将Q1与Q3之间的间距称为IQR,当样本偏离上四分位1.5倍的IQR(或是偏离下四分位数1.5倍的IQR)的情况下,将样本视为是一个离群点。不同于基于正态假设的三倍标准差,通常情况下,箱形图对于样本的潜在数据分布没有任何假定,能够描述出样本的离散情况,且对样本中包含的潜在异常样本有较高的容忍度。对于有偏数据,Boxplot进行校准后建模更加符合数据分布[7]。
7.3 极值理论
真实世界的数据很难用一种已知的分布来概括,例如对于某些极端事件(异常),概率模型(例如高斯分布)往往会给出其概率为0。极值理论[8]是在不基于原始数据的任何分布假设下,通过推断我们可能会观察到的极端事件的分布,这就是极值分布(EVD)。其数学表达式如下(互补累积分布函数公式):其中t代表样本的经验阈值,对于不同场景可以设置不同取值,,分别是广义帕累托分布中的形状参数与尺度参数,在给定样本超过人为设定的经验阈值t的情况下,随机变量X-t是服从广义帕累托分布的。通过极大似然估计方法我们可以计算获得参数估计值与 ,并且通过如下公式来求取模型阈值: 上述公式中q代表风险参数,n是所有样本数量,Nt是满足x-t>0的样本数量。由于通常情况下对于经验阈值t的估计没有先验的信息,因此可以使用样本经验分位数来替代数值t,这里经验分位数的取值可以根据实际情况来选择。


